Time Value of Money in Fixed Income and Equity

In general, the relationship between a current or present value (PV) and future value (FV) of a cash flow, where r is the stated discount rate per period and t is the number of compounding periods, is as follows:

FV_t = PV(1 + r)^t

If the number of compounding periods t is very large, that is, $t\rightarrow \infin$ , we compound the initial cash flow on a continuous basis as follows:

FV_t = PV\mathrm{e}^{rt}

Conversely, present values can be expressed in future value terms:

PV = FV_t(1 + r)^{-t}

The continuous time equivalent expression:

PV = FV_t\mathrm{e}^{-rt}

Fixed-Income Instruments and the Time Value of Money

Fixed-income instruments are debt instruments, such as a bond or a loan, that represent contracts under which an issuer borrows money from an investor in exchange for a promise of future repayment. The discount rate for fixed-income instruments is an interest rate, and the rate of return on a bond or loan is often referred to as its yield-to-maturity (YTM).

Cash flows associated with fixed-income instruments usually follow one of three general patterns:

Discount: An investor pays an initial price (PV) for a bond or loan and receives a single principal cash flow (FV) at maturity. The difference (FV − PV) represents the interest earned over the life of the instrument.
Periodic Interest: An investor pays an initial price (PV) for a bond or loan and receives interest cash flows (PMT) at pre-determined intervals over the life of the instrument, with the final interest payment and the principal (FV) paid at maturity.
Level Payments: An investor pays an initial price (PV) and receives uniform cash flows at pre-determined intervals (A) through maturity which represent both interest and principal repayment.

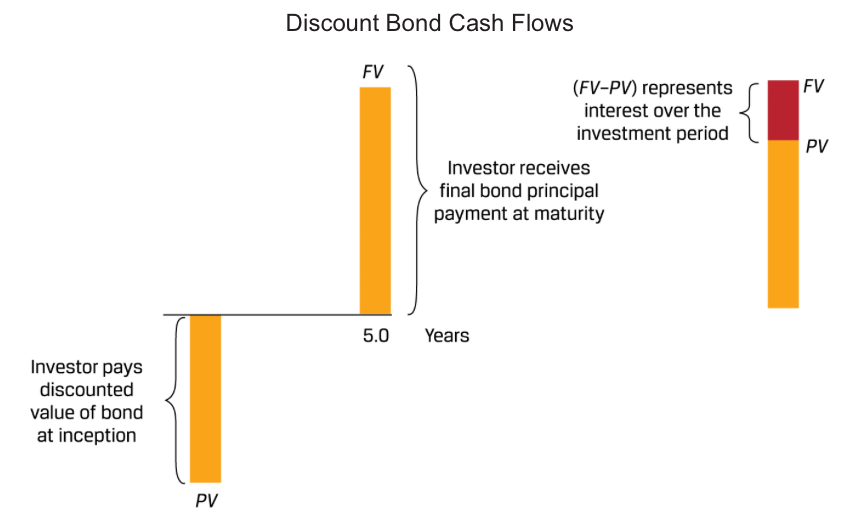
The present value (PV) calculation for a discount bond with principal (FV) paid at time with a market discount rate of r per period is:

PV(\text{Discount Bond}) = \frac{FV_t}{(1 + r)^t}

The investor’s sole source of return is the difference between the price paid (PV) and full principal (Fv) received at maturity. This type of bond is often referred to as a zero-coupon bond given the lack of intermediate interest cash flows, which for bonds are generally referred to as coupons.

Coupon Instrument

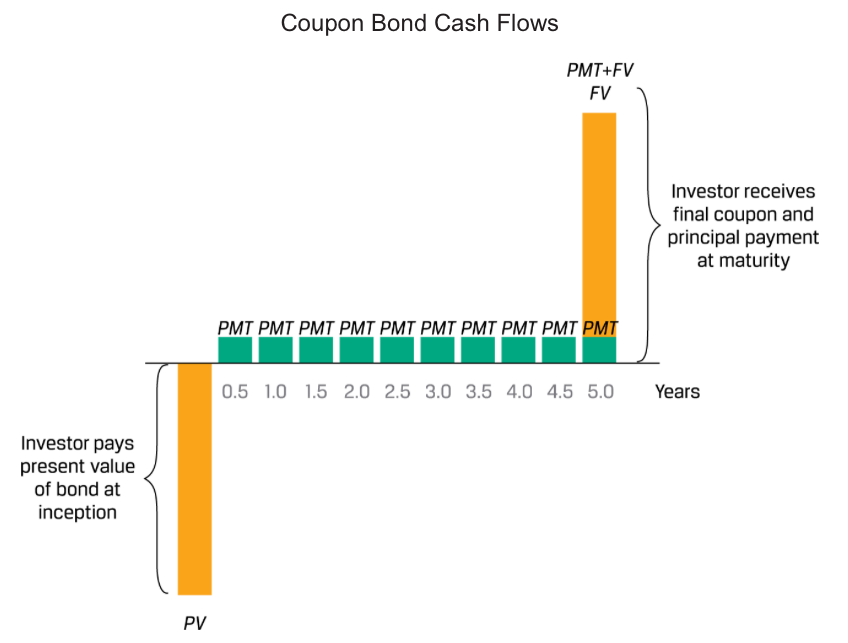
Pricing a coupon bond extends the single cash flow calculation for a discount bond to a general formula for calculating a bond’s price (PV) given the market discount rate on a coupon date, as follows:

PV(Coupon\ Bond) = \frac{PMT_1}{(1+r)^1} + \frac{PMT_2}{(1+r)^2} + \dots + \frac{PMT_N+FV_N}{(1+r)^N}

A perpetual bond is a less common type of coupon bond with a stated maturity date. Most perpetual bonds are issued by companies to obtain equity-like financing and often include redemption features. As $N \rightarrow\infin$ , we can simplify this to solve for the present value of a perpetuity (or perpetual fixed periodic cash flow without early redemption), where r > 0, as follows:

PV(Perpetual\ Bond) = \frac{PMT}{r}

Annuity Instruments

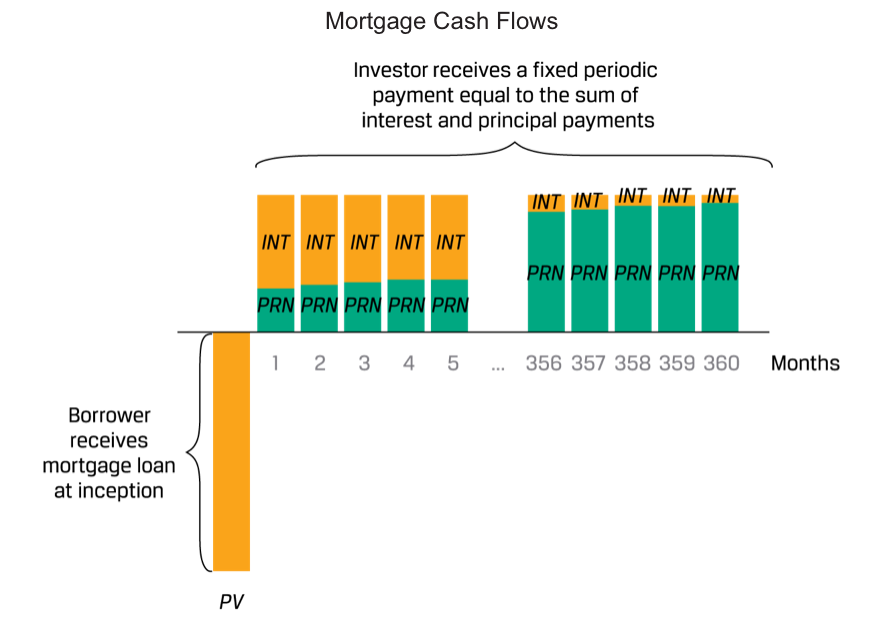
We may calculate the periodic annuity cash flow (A), which occurs at the end of each respective period, as follows:

A = \frac{r(PV)}{1-(1+r)^{-t}}

where:

A = periodic cash flow,

r = market interest rate per period,

PV = present value or principal amount of loan or bond, and

t = number of payment periods.

Equity Instruments and the Time Value of Money

Equity investments, such as preferred or common stock, represent ownership shares in a company which entitle investors to receive any discretionary cash flows in the form of dividends. Unlike fixed-income instruments, equity investments have no maturity date and are assumed to remain outstanding indefinitely, or until a company is sold, restructured, or liquidated. One way to value a company’s shares is by discounting expected future cash flows using an expected rate of return (r). These cash flows include any periodic dividends received plus the expected price received at the end of an investment horizon.

Common assumptions associated with valuing equity instruments based upon dividend cash flows often follow one of three general approaches:

Constant Dividends: An investor pays an initial price (PV) for a preferred or common share of stock and receives a fixed periodic dividend (D).
Constant Dividend Growth Rate: An investor pays an initial price (PV) for a share of stock and receives an initial dividend in one period (D_t+1), which is expected to grow over time at a constant rate of g.
Changing Dividend Growth Rate: An investor pays an initial price (PV) for a share of stock and receives an initial dividend in one period (D_t+1). The dividend is expected to grow at a rate that changes over time as a company moves from an initial period of high growth to slower growth as it reaches maturity.

The price of a preferred or common share expected to pay a constant periodic dividend is an infinite series that simplifies to the formula for the present value of a perpetuity shown and is similar to the valuation of a perpetual bond.

PV_t = \sum_{i=1}^\infin{\frac{D_t}{(1+r)^i}}

PV_t = \frac{D_t}{r}

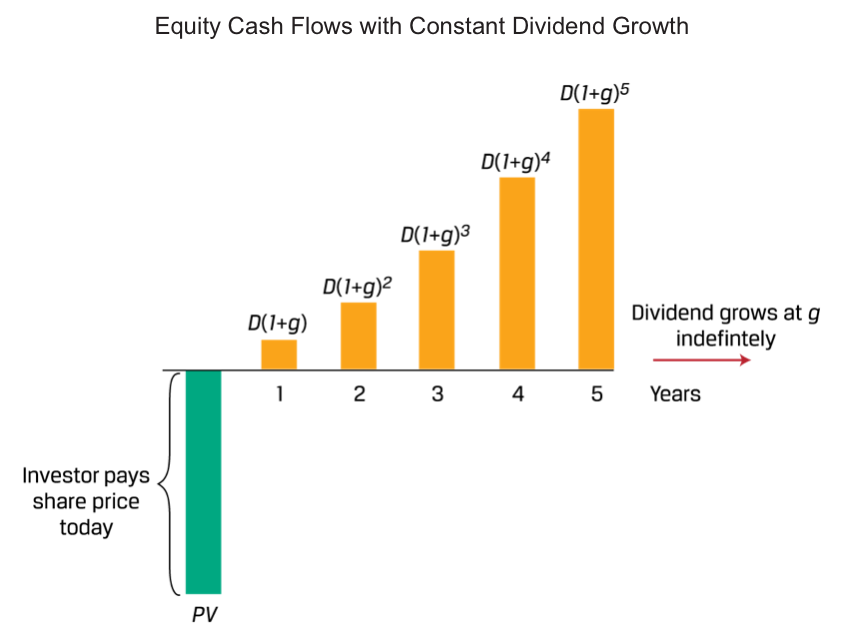
If dividends grow at a rate of g per period and are paid at the end of each period, the next dividend (at time t+1) may be shown as follows:

D_{t+1} = D_t(1+g)

or generally in i periods as:

D_{t+i} = D_t(1+g)^i

If dividend cash flows continue to grow at g indefinitely,

PV_t = \sum_{i=1}^\infin{\frac{D_t(1+g)^i}{(1+r)^i}}

which simplifies to:

PV_t =\frac{D_t(1+g)}{r-g} = \frac{D_{t+1}}{r-g}

where r – g > 0.

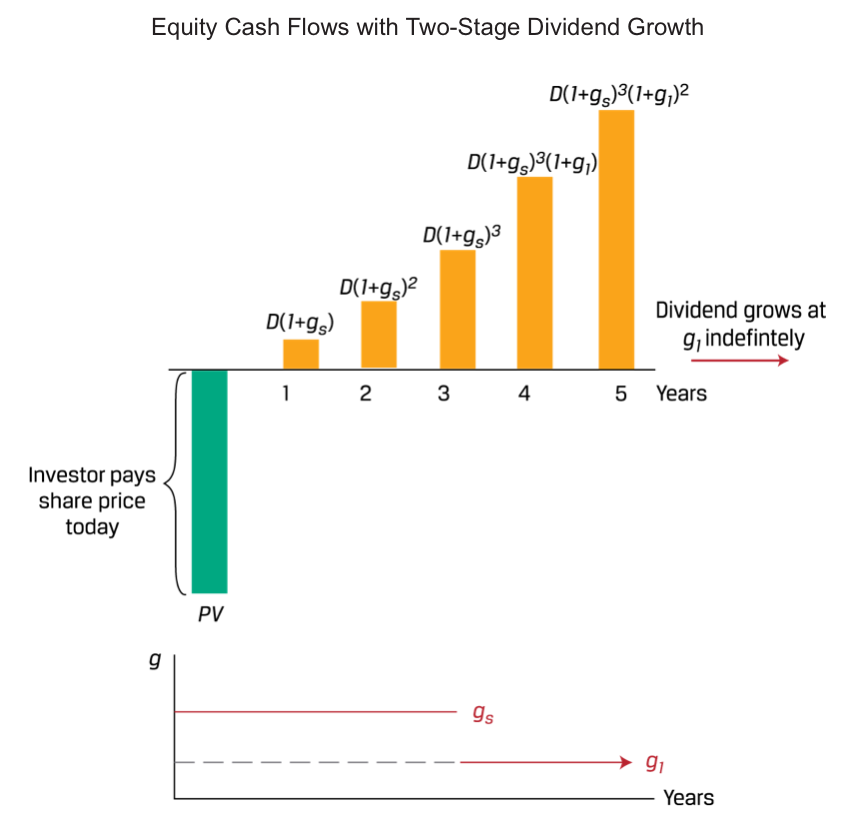
A company with an initial higher short-term dividend growth of $g_s$ for the first three years, followed by lower long-term growth ( $g_i, where\ g_s >g_i$ ) indefinitely thereafter. If we generalise the initial growth phase to n periods followed by indefinite slower growth at $g_i$ ,