Probability sampling gives every member of the population an equal chance of being selected.
Non-probability sampling depends on factors other than probability considerations, such as a sampler’s judgment or the convenience of access data. Consequently, there is a significant risk that non-probability sampling might generate a non-representative sample.
Simple Random Sampling
A sampling plan is the set of rules used to select a sample. The basic type of sample from which we can draw statistically sound conclusions about a population is the simple random sample.
A simple random sample is a subset of a larger population created in such a way that each element of the population has an equal probability of being selected to the subset.
The procedure of drawing a sample to satisfy the definition of a simple random sample is called simple random sampling. Simple random sampling is particularly useful when data in the population is homogeneous—that is, the characteristics of the data or observations (e.g., size or region) are broadly similar.
Systematic sampling can be used when we cannot code (or even identify) all the members of a population. With systematic sampling, we select every Kth member until we have a sample of the desired size.
Sampling error is the difference between the observed value of a statistic and the quantity it is intended to estimate as a result of using subsets of the population.
Sampling distribution of a statistic is the distribution of all the distinct possible values that the statistic can assume when computed from samples of the same size randomly drawn fro mthe same population.
Stratified Random Sampling
In stratified random sampling, the population is divided into subpopulations (strate) based on one or more classification criteria. Simple random samples are then drawn from each stratum in sizes proportional to the relative size of each stratum in the population.
Indexing is an investment strategy in which an investor constructs a portfolio to mirror the performance of a specified index.
Cluster Sampling
Cluster Sampling requires the division or classification of the population into subpopulation groups, called clusters.
In this method, the population is divided into clusters, each of which is essentially a mini-representation of the entire populations.
Then certain clusters are chosen as a whole using simple random sampling. If all the members in each sampled cluster are sampled, this sample plan is referred to as one-stage cluster sampling. If a subsample is randomly selected from each selected cluster, then the plan is referred as two-stage cluster sampling.
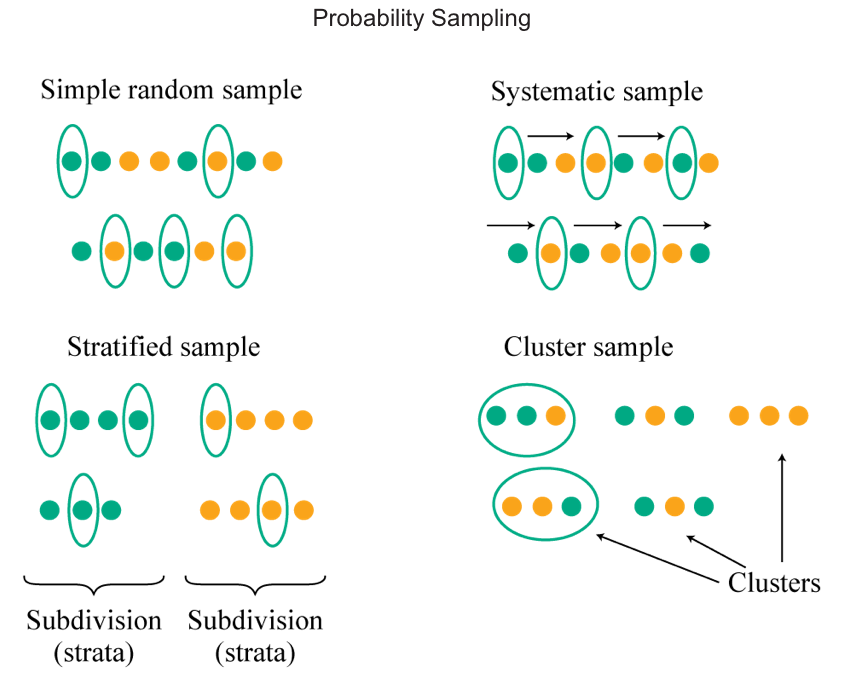
A major difference between cluster and stratified random samples is that in cluster sampling, a whole cluster is regarded as a sampling unit and only sampled clusters are included. In stratified random sampling, however, all the strata are included and only specific elements within each stratum are then selected as sampling units.
Non-Probability Sampling
- Convenience Sampling: In this method, an element is selected from the population based on whether or not it is accessible to a researcher or on how easy it is for a researcher to access the element. The samples are not necessarily representative of the entire population, and hence the level of sampling accuracy could be limited. The advantage of convenience sampling is that data can be collected quickly at a low cost. In situations such as the preliminary stage of research or in circumstances subject to cost constraints, convenience sampling is often used as a time-efficient and cost-effective sampling plan for a small-scale pilot study before testing a large-scale and more representative sample.
- Judgmental Sampling: This sampling process involves selectively handpicking elements from the population based on a researcher’s knowledge and professional judgment. Sample selection under judgmental sample can be affected by the bias of the researcher and might lead to skewed results that do not represent the whole population. In circumstances where there is a time constraint, however, or when the specialty of researchers is critical to select a more representative sample than by using other probability or non-probability sampling methods, judgmental sampling allows researchers to go directly to the target population of interest. For example, when auditing financial statements, seasoned auditors can apply their sound judgment to select accounts or transactions that can provide sufficient audit coverage.









