55 Questions (About 15 Questions on exam)
Reference:
1. The nominal risk-free rate is best described as the sum of the real risk-free rate and a premium for:
A. maturity.
B. liquidity.
C. expected inflation.
C is correct. The nominal risk-free rate is approximated as the sum of the real risk-free interest rate and an inflation premium.
The nominal rate is often approximated as the sum of the real risk-free rate plus an inflation premium.
2. Which of the following risk premiums is most relevant in explaining the difference in yields between 30-year bonds issued by the US Treasury and 30-year bonds issued by a small, private US corporate issuer?
A. Inflation
B. Maturity
C. Liquidity
C is correct. US Treasury bonds are highly liquid, whereas the bonds of small issuers trade infrequently and the interest rate includes a liquidity premium. This liquidity premium reflects the relatively high costs (including the impact on price) of selling a position. As the two bond issues have the same 30-year maturity, the observed difference in yields would not be solely explained by maturity. Further, the inflation premium embedded in the yield of both bonds is likely to be similar given they are both US-based bonds with the same maturity.
3. Consider the following annual return for Fund Y over the past five years:
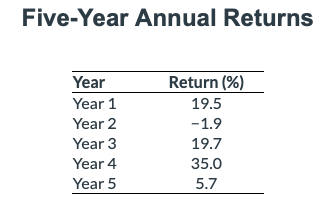
The geometric mean return for Fund Y is closest to:
A. 14.9 percent.
B. 15.6 percent.
C. 19.5 percent.
A is correct. The geometric mean return for Fund Y is calculated as follows:
= [(1 + 0.195) × (1 − 0.019) × (1 + 0.197) × (1 + 0.350) × (1 + 0.057)](1/5) − 1= 14.9%.
4. A portfolio manager invests EUR5,000 annually in a security for four years at the following prices:
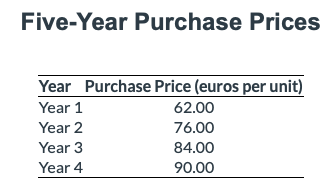
The average price is best represented as the:
A. harmonic mean of EUR76.48.
B. geometric mean of EUR77.26.
C. arithmetic average of EUR78.00.
A is correct. The harmonic mean is appropriate for determining the average price per unit as it gives equal weight to each data point and reduces the potential influence of outliers. It is calculated as follows:
4/[(1/62.00) + (1/76.00) + (1/84.00) + (1/90.00)] = EUR76.48.
The simple way to find an answer is to directly find the keywords “harmonic mean”. SAVE TIME!
5. Which of the following statements regarding arithmetic and geometric means is correct?
A. The geometric mean will exceed the arithmetic mean for a series with non-zero variance.
B. The geometric mean measures an investment’s compound rate of growth over multiple periods.
C. The arithmetic mean measures an investment’s terminal value over multiple periods.
B is correct. The geometric mean compounds the periodic returns of every period, giving the investor a more accurate measure of the terminal value of an investment.
6. A fund receives investments at the beginning of each year and generates returns for three years as follows:

Which return measure over the three-year period is negative?
A. Geometric mean return
B. Time-weighted rate of return
C. Money-weighted rate of return
C is correct. The money-weighted rate of return considers both the timing and amounts of investments into the fund. To calculate the money-weighted rate of return, tabulate the annual returns and investment amounts to determine the cash flows.
| Year | 1 | 2 | 3 |
|---|---|---|---|
| Balance from previous year | 0 | USD1,150 | USD4,560 |
| New investment | USD1,000 | USD2,850 | USD40,440 |
| Net balance at the beginning of year | USD1,000 | USD4,000 | USD45,000 |
| Investment return for the year | 15% | 14% | −4% |
| Investment gain (loss) | USD150 | USD560 | −USD1,800 |
| Balance at the end of year | USD1,150 | USD4,560 | USD43,200 |
CF0 = –USD1,000, CF1 = –USD2,850, CF2 = –USD40,440, CF3 = +USD43,200.
Solving for IRR results in a value of IRR = −2.22 percent.
Note that A and B are incorrect because the time-weighted rate of return (TWR) of the fund is the same as the geometric mean return of the fund and is positive:
The simplest way to find the answer is to understand that an annualised time-weighted return can be calculated as the geometric mean of N anaual return, which can hardly be negative. Therefore, the answer must be C.
7. At the beginning of Year 1, a fund has USD10 million under management; it earns a return of 14 percent for the year. The fund attracts another net USD100 million at the start of Year 2 and earns a return of 8 percent for that year. The money-weighted rate of return of the fund is most likely to be:
A. less than the time-weighted rate of return.
B. the same as the time-weighted rate of return.
C. greater than the time-weighted rate of return.
A is correct. Computation of the money-weighted return, r, requires finding the discount rate that sums the present value of cash flows to zero. Because most of the investment came during Year 2, the money-weighted return will be biased toward the performance of Year 2 when the return was lower. The cash flows are as follows:
CF0 = −10
CF1 = −100
CF2 = +120.31
The terminal value is determined by summing the investment returns for each period [(10 × 1.14 × 1.08) + (100 × 1.08)].
This results in a value of IRR = 8.53 percent.
The time-weighted return of the fund is calculated as follows:
8. An investor is evaluating the returns of three recently formed ETFs. Selected return information on the ETFs is presented in Exhibit 1:
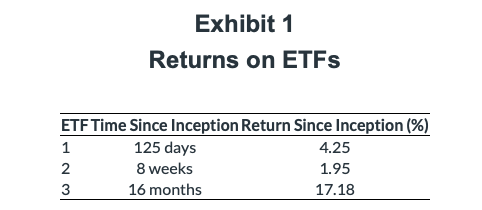
Which ETF has the highest annualised rate of return?
A. ETF 1
B. ETF 2
C. ETF 3
B is correct. The annualised rate of return for
ETF 1 annualised return = (1.0425365/125) – 1 = 12.92%
ETF 2 annualised return = (1.019552/8) − 1 = 13.37%
ETF 3 annualised return = (1.171812/16) – 1 = 12.63%
Despite having the lowest value for the periodic rate, ETF 2 has the highest annualised rate of return because of the reinvestment rate assumption and the compounding of the periodic rate.
9. The price of a stock at t = 0 is USD208.25 and at t = 1 is USD186.75. The continuously compounded rate of return, r1,T for the stock from t = 0 to t = 1 is closest to:
A. –10.90 percent.
B. –10.32 percent.
C. 11.51 percent.
A is correct. The continuously compounded return from t = 0 to t = 1 is r 0,1 = ln(S1 /S 0) = ln(186.75/208.25) = –0.10897 = –10.90%.
10. A USD25 million equity portfolio is financed 20 percent with debt at a cost of 6 percent annual cost. If that equity portfolio generates a 10 percent annual total investment return, then the leveraged return is:
A. 11.0 percent.
B. 11.2 percent.
C. 13.2 percent
A is correct.
11. An investment manager’s gross return is:
A. an after-tax nominal, risk-adjusted return.
B. the return earned by the manager prior to deduction of trading expenses.
C. an often used measure of an investment manager’s skill because it does not include expenses related to management or administration.
C is correct. Gross returns are calculated on a pre-tax basis; trading expenses are accounted for in the computation of gross returns as they contribute directly to the returns earned by the manager. A is incorrect because investment managers’ gross returns are pre-tax and not adjusted for risk. B is incorrect because managers’ gross returns do reflect the deduction of trading expenses since they contribute directly to the return earned by the manager.
12. The strategy of using leverage to enhance investment returns:
A. amplifies gains but not losses.
B. doubles the net return if half of the invested capital is borrowed.
C. increases total investment return only if the return earned exceeds the borrowing cost.
C is correct. The use of leverage can increase an investor’s return if the total investment return earned on the leveraged investment exceeds the borrowing cost on debt. A is incorrect because leverage amplifies both gains and losses. B is incorrect because, if half of the invested capital is borrowed, then the investor’s gross (not net) return would double.
13. At the beginning of the year, an investor holds EUR10,000 in a hedge fund. The investor borrowed 25 percent of the purchase price, EUR2,500, at an annual interest rate of 6 percent and expects to pay a 30 percent tax on the return she earns from his investment. At the end of the year, the hedge fund reported the information in Exhibit 1:

The investor’s after-tax return on the hedge fund investment is closest to:
A. 3.60 percent.
B. 3.98 percent.
C. 5.00 percent.
C is correct. The first step is to compute the investor’s net return from the hedge fund investment. The net return is the fund’s gross return less managerial and administrative expenses of 1.60 percent, or 8.46% – 1.60% = 6.86%. Note that trading expenses are already reflected in the gross return, so they are not subtracted.
The second step is to compute the investor’s leveraged return (the investor borrowed EUR2,500 (25 percent) of the purchase), calculated as follows:
The final step is to compute the after-tax return:
After-tax return = 7.15% (1 – 0.30) = 5.00%.
14. An investor purchases one share of stock for $85. Exactly one year later, the company pays a dividend of $2.00 per share. This is followed by two more annual dividends of $2.25 and $2.75 in successive years. Upon receiving the third dividend, the investor sells the share for $100. The money-weighted rate of return on this investment is closest to:
A. 7.97%.
B. 8.15%.
C. 8.63%.
A Incorrect. It adds all three dividends together and (incorrectly) calculates the HPR of the investment as (2 + 2.25 + 102.75)/85 = 1.25882353. Then the third root of this number is taken and 1 is subtracted. The result is 7.97%.
B Correct. The money-weighted rate of return is the internal rate of return (IRR) of the cash flows associated with the investment. The following figure represents the timeline for the problem:

Using the cash flow (CF) function of a financial calculator: CF0 = −85, CF1 = 2, CF2 = 2.25, CF3 = 102.75; and solving for IRR: IRR = 8.15%.
C Incorrect. It is calculated by subtracting 1 from 1.25882353 (see Feedback A) and dividing the remainder by 3. The result is 8.63%.
15. The liquidity premium can best be described as compensation to investors for the:
A. risk of loss relative to an investment’s fair value if the investment needs to be converted to cash quickly.
B. increased sensitivity of the market value of debt to a change in market interest rates as maturity is extended.
C. possibility that the borrower will fail to make a promised payment at the contracted time and in the contracted amount.
A Correct. The liquidity premium compensates investors for the risk of loss relative to an investment’s fair value if the investment needs to be converted to cash quickly.
B Incorrect because the compensation to investors for the increased sensitivity of the market value of debt to a change in market interest rates as maturity is extended is the maturity premium.
C Incorrect because the compensation to investors for the possibility that the borrower will fail to make a promised payment at the contracted time and in the contracted amount is the default risk premium.
16. Once an investor chooses a particular course of action, the value forgone from alternative actions is best described as a(n):
A. sunk cost.
B. required return.
C. opportunity cost.
Correct. An opportunity cost is the value that investors forgo by choosing a particular course of action.
17. The quarterly returns on a portfolio are as follows:
| Quarter | 1 | 2 | 3 | 4 |
| Return | 20% | -20% | 10% | -10% |
The time-weighted rate of return of the portfolio is closest to:
A. −5.0%.
B. −1.3%.
C. 0.0%.
A Correct because the time-weighted rate of return of this portfolio is (1 + r1)(1 + r2)(1 + r3)(1 + r4) − 1, where , r1 = holding period return (HPR) for the first quarter, second quarter, and so on.
= (1 + 0.20)(1 − 0.20)(1 + 0.10)(1 − 0.10) − 1
= −4.96% ≈ −5.0%
B Incorrect because −1.3% would represent the time-weighted rate of return if the returns given in the table had been yearly rather than quarterly returns. Calculated as:
rTW = [(1 + r1)(1 + r2)(1 + r3)(1 + r4)]1/N − 1
= [(1.20)(0.80)(1.10)(0.90)]1/4 − 1 = −1.2638% ≈ −1.3%
C Incorrect because 0.0% represents simple addition of gain and loses. Calculated as:
+20% − 20% + 10% − 10% = 0.0%
18. The annualised return for an investor who has achieved a return of 5% over a six-week period is closest to:
A. 43.33%.
B. 52.63%.
C. 54.24%.
A Incorrect. Its return is calculated as 5% × (52/6) = 43.33%
B Correct. Annualised return is calculated as (1 + 5%)52/6 – 1 = 52.63.
C Incorrect. Its return is calculated as e5%(52/6) – 1 = 54.24%.
19. An investor deposits £2,000 into an account that pays 6% per annum compounded continuously. The value of the account at the end of four years is closest to:
A. £2,525.
B. £2,542.
C. £2,854.
A Incorrect. It uses annual compounding: 2,000 × (1 + 0.06)4 = 2,524.95.
B Correct. The future value (FV) of a given lump sum, calculated using continuous compounding, is: FV = PVerN = 2,000 × e0.06 × 4 = £2,542.49 ~ £2,542.
C Incorrect. It is calculated as: ln(0.06 × 4) × 2,000 = −2,854.23 and ignores the negative sign of the logarithm.
20. Using a discount rate of 5%, compounded monthly, the present value (PV) of $5,000 to be received three years from today is closest to:
A. $4,250.
B. $4,319.
C. $4,305.
A Incorrect. It is calculated as PV = 5,000[1 − (0.05 × 3)] = 4,250.
B Incorrect. It is calculated without monthly compounding (N = 3, I/Y = 5). Alternatively:
5,000(1 + 0.05)(−3) = 4,319 (rounded)
C Correct. PV = FVN(1 + rs/m)−mN. In this case, PV = $5,000(1 + 0.05/12)(−12×3) = $4,304.88.
Using a financial calculator: FV = $5,000, N = 36, I/Y = 5/12, PMT = 0, and solve for PV.21.
21. Assume the following:
- The real risk-free rate of return is 3%.
- The expected inflation premium is 5%.
- The market-determined interest rate of a security is 12%.
The sum of the default risk premium, liquidity premium, and maturity premium for the security is closest to:
A. 4%.
B. 8%.
C. 10%.
A Correct. The market-determined interest rate is equal to the real risk-free rate of return plus an inflation premium plus risk premiums for default risk, liquidity, and maturity. In this case, 12 = 3 + 5 + X. Solving for X: X = 4.
B Incorrect. Eight percent is the sum of the real risk-free rate and expected inflation.
C Incorrect. 10% =12% − (5% − 3%)
22. The minimum rate of return an investor must receive in order to accept an investment is best described as the:
A. expected return.
B. internal rate of return.
C. required rate of return.
A Incorrect. The required rate of return is the minimum rate of return an investor must receive in order to accept an investment. The expected return is based on the expected value of a random variable and is not the minimum rate of return an investor must receive in order to accept an investment (i.e., the expected return could also be negative).
B Incorrect. The required rate of return is the minimum rate of return an investor must receive in order to accept an investment. The internal rate of return is the discount rate that makes net present value equal to zero.
C Correct. The required rate of return is the minimum rate of return an investor must receive in order to accept an investment.
23. Over the past four years, a portfolio experienced returns of −8%, 4%, 17%, and −12%. The geometric mean return of the portfolio over the four-year period is closest to:
A. −0.37%.
B. 0.25%.
C. 0.99%.
A Correct. Add one to each of the given returns, then multiply them together and take the fourth root of the resulting product. 0.92 × 1.04 × 1.17 × 0.88 = 0.985121; 0.985121 raised to the 0.25 power is 0.996259. Subtracting one and multiplying by 100 gives the correct geometric mean return: [(0.92 × 1.04 × 1.17 × 0.88)0.25 − 1] × 100 = −0.37%.
B Incorrect because it is the arithmetic mean of the four numbers.
C Incorrect because it is the solution to: (0.92 × 1.04 × 1.17 × 0.88) = 0.99 (rounded).
24. A portfolio provides the following returns over a five-year period.
| Year | 1 | 2 | 3 | 4 | 5 |
| Return | 10% | -25% | 8% | 5% | 7% |
The average compound rate of return of the portfolio across the five-year period is closest to:
A. −9.31%.
B. 0.02%.
C. 1.00%.
A Incorrect. It is the geometric mean of the given values (i.e., does not add 1 to each return): (0.10 × −0.25 × 0.08 × 0.05 × 0.07)1/5 = −9.31%: it also ignores the negative sign inside the brackets, but applies it to the answer.
B Correct. The geometric mean return is the correct approach to calculate portfolio average returns across a period of time:
where
RG = the geometric mean return
T = 5 and is the length of the period
t = the index of time (i.e., t = 1 for Year 1, t = 2 for Year 2, …)
Rt = the return during period t
In this problem, the geometric mean return is:
RG = [(1 + 0.10) × (1 − 0.25) × (1 + 0.08) × (1 + 0.05) × (1 + 0.07)]1/5 − 1
= (1.10 × 0.75 × 1.08 × 1.05 × 1.07)1/5 − 1
= 0.02%.
C Incorrect. It is the arithmetic average: (0.10 − 0.25 + 0.08 + 0.05 + 0.07)/5 = 1.00%.
25. If the price of a stock goes from $15.00 to $16.20 in one year, the continuously compounded rate of return is closest to:
A. 7.70%.
B. 8.33%.
C. 8.00%.
A Correct. The continuously compounded rate of return is calculated with the following formula: r0,T = ln(ST/S0)
where
r0,T = r0,1 = and is the continuously compounded rate of return from time 0 to time T (1 year)
S0 = 15.00 and is the price of the stock at time 0
ST = 16.20 and is the price of the stock at time T (1 year)
The continuously compounded rate of return is: r0,1 = ln(16.20/15.00) = 7.70%.
Alternatively, the end of period price, 16.20 can be found from 15.00 × e0.077×1.
B Incorrect. It is calculated as: exp(Holding period return) − 1= exp[(16.20/15.00) − 1] − 1 = exp(8.00%) − 1 = 8.33%.
C Incorrect. It is the holding period return: (16.20/15.00) − 1 = 8.00%.
26. Investor A and Investor B invest in a fund for two years:
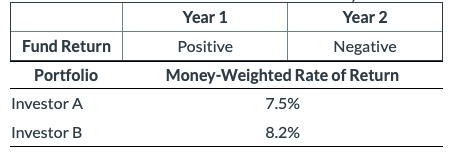
Given the information in the table, which of the following is least likely to be an explanation for the difference between the two money-weighted rates of return?
A. Investor A increased the investment in the fund at the end of year 1 whereas investor B did not make any additions or withdrawals.
B. Investor B decreased the investment in the fund at the end of year 1 whereas investor A did not make any additions or withdrawals.
C. The investors invested different amounts at inception and afterward did not make any additions or withdrawals.
A Incorrect. If investor A increases the investment in the fund at the end of year 1 and investor B does not make any additions or withdrawals, then investor A will have a lower MWR than investor B because in year 2 the fund underperformed with respect to year 1. This is therefore incorrect since the stem asks for the least likely explanation.
B Incorrect. If investor A increases the investment in the fund at the end of year 1 and investor B does not make any additions or withdrawals, then investor A will have a lower MWR than investor B because in year 2 the fund underperformed with respect to year 1. This is therefore incorrect since the stem asks for the least likely explanation.
C Correct. The money-weighted rate of return (MWR) is sensitive to the additions and withdrawals of funds in a portfolio over the course of an investment. If, at inception, investors A and B invest amounts of different size in the same fund but then neither add nor withdraw any cash for two years, they will obtain exactly the same MWR. In contrast, if investor A increases the investment in the fund at the end of year 1 and investor B does not make any additions or withdrawals, then Investor A will have a lower MWR than investor B because in year 2 the fund underperformed with respect to year 1. By the same token, if investor B decreases the investment at the end of year 1 and investor A does not make any additions or withdrawals, then investor B will have a higher MWR than investor A because she decreased the investment before an underperforming year.
27. An investment in 10,000 common shares of a company for one year earned a 15.5% return. The investor received a $2,500 dividend just prior to the sale of the shares at $24 per share. The price that the investor paid for each share one year earlier was closest to:
A. $20.80.
B. $20.50.
C. $21.00.
A Incorrect. It ignores dividend.
0.155 = (24 − P0)/P0
P0 = $20.78
B Incorrect. It is calculated as HPR = (P1 − P0 + D1)/P1
0.155 = (24 − P0 + 0.25)/24
P0 = $20.53
C Correct. Holding period return, HPR = (P1 − P0 + D1)/P0 where
P0 = initial investment
P1 = price received at the end of holding period
D1 = dividend paid by the investment at the end of holding period
= $2,500/10,000 shares = $0.25/shares
0.155 = (24 − P0 + 0.25)/P0, and solving for P0
P0 = $20.99 ~ $21.00
28. Consider the investment in the following table:
| Start of Year 1 | One share purchased at $100 |
| End of Year 1 | $5.00 dividend/share paid and one additional share purchased at $125 |
| End of Year 2 | $5.00 dividend/share paid and both shares are sold for $140 per share |
Assuming dividends are not reinvested, compared with the time-weighted return, the money-weighted return is:
A. lower.
B. the same.
C. higher.
A Correct. The following table represents cash flows of the investment:
| Year | Contribution | Start-of-Year Value after Contribution | End-of-Year Dividend | End-of-Year Value after Dividend |
| 1 | 1 × $100 | 1 × $100 = $100 | 1 × $5 = $5 | $125 + 5 = $130 |
| 2 | 1 × $125 | 2 × $125 = $250 | 2 × $5 = $10 | (2 × 140) + 10 = $290 |
The time-weighted rate of return (TWR) on this investment is found by taking the geometric mean of the two holding period returns (HPRs): TWR = [(1 + HPRYear 1) × (1 + HPRYear 2)]1/2 − 1 where
HPRYear 1 = ($125 − $100 + $5)/$100 = 30.0%
HPRYear 2 = ($280 − $250 + $10)/$250 = 16.0%
TWR = [(1 + 0.30) × (1 + 0.16)]1/2 − 1 = 22.80%
The money-weighted rate of return (MWR) is the internal rate of return (IRR) of the cash flows associated with the investment:
, where r = MWR.
Using the cash flow (CF) function of a financial calculator:
CF0 = −100, CF1 = (−125 + 5), CF2 = (280 + 10), and solving for IRR: MWR or IRR = 20.55%.
The difference between the TWR and MWR of this investment = 22.80% − 20.55% = 2.25%, or 225 bps, with MWR being lower than TWR.
B Incorrect. The difference between MWR and TWR is either higher or lower, and could hardly be equal.
C Incorrect.
29. An investor purchases 100 shares of stock at $40 per share. The investor holds the shares for exactly one year and then sells all of them at $41.50 per share. On the date of sale, the investor receives dividends totaling $200. The holding period return (HPR) on the investment is closest to:
A. 8.75%.
B. 3.75%.
C. 8.43%.
A Correct. HPR = (P1 − P0 + D1)/P0. In this problem: (41.50 − 40 + 2)/40 = 8.75%. Note: dividends totaled $200, representing a $2 per share dividend ($200 total dividend/100 shares).
B Incorrect. It is calculated as (41.50 − 40)/40 = 3.75% (ignores dividends).
C Incorrect. It is calculated as (41.50 − 40 + 2)/41.50 = 8.43% (wrong denominator).
30. An analyst observes that the historic geometric nominal return for equities is 9%. Given a real return of 1% for riskless Treasury bills and annual inflation of 2%, the real rate of return and risk premium for equities are closest to:
A. 7.9% and 5.8%.
B. 6.9% and 7.9%.
C. 6.9% and 5.8%.
A Incorrect.
[(1 + 0.09)/(1 + 0.01)] – 1 = 7.9%, and [(1 + 0.079)/(1 + 0.02)] – 1 = 5.8%
B Incorrect.
[(1 + 0.09)/(1 + 0.02)] – 1 = 6.9%, and [(1 + 0.09)/(1 + 0.01)] – 1 = 7.9%
C Correct.
(1 + nominal return on risky asset) = (1 + real return on risky asset)(1 + inflation premium)
Therefore, [(1 + 0.09)/(1 + 0.02)] – 1 = 6.9% real return on risky asset.
(1 + real return on risky asset) = (1 + real risk-free rate)(1 + risk premium)
Therefore, [(1 + 0.069)/(1 + 0.01)] – 1 = 5.8% risk premium.
31. The return measure that best allows one to compare asset returns earned over different length time periods is the:
A. holding period return.
B. annualised return.
C. net portfolio return.
A Incorrect. The holding period return is defined as the return earned from holding an asset for a single specified period of time.
B Correct. The annualised return is an average return measure that can be calculated using return data for a period that is shorter (or longer) than one year. In many cases, it is most convenient to annualise all available returns in order to compare returns when the time periods during which a return is earned or computed vary. It reflects the return that would be earned over a one-year period, assuming that money can be reinvested repeatedly while earning a similar return.
C Incorrect. The portfolio return is simply a weighted average of the returns of the individual investments or assets in a portfolio. Returns to different portfolios may be calculated over different time periods and may not be comparable.
32. The 15-month holding period return for a security is 12%. Its annualised return is closest to:
A. 9.49%.
B. 9.60%.
C. 10.03%.
A (1 + 0.12)12/15 – 1 = 9.49%
B Incorrect. 12% × 12/15 = 9.60%.
C Incorrect. (1 + 0.12/15)12 – 1 = 10.03%.
33. For a given dataset with different non-negative observations, which of the following will have the largest value?
A. Harmonic mean
B. Arithmetic mean
C. Geometric mean
A Incorrect because for a given dataset with different observations, the harmonic mean has the smallest value among harmonic, geometric, and arithmetic means. Unless all the observations in a dataset have the same value, the harmonic mean is less than the geometric mean, which, in turn, is less than the arithmetic mean.
B Correct because the arithmetic mean of a given dataset with different observations is higher than the harmonic and geometric means. Unless all the observations in a dataset have the same value, the harmonic mean is less than the geometric mean, which, in turn, is less than the arithmetic mean.
C Incorrect because for a given dataset with different observations, the geometric mean is larger than the harmonic mean but smaller than the arithmetic mean. Unless all the observations in a dataset have the same value, the harmonic mean is less than the geometric mean, which, in turn, is less than the arithmetic mean.
34. An investor is considering buying a US T-bill. If the real risk-free rate is 1% and the inflation premium is 2%, the investor’s opportunity cost of failing to make this investment is closest to:
A. 1%.
B. 2%.
C. 3%.
A Incorrect because interest rates can be considered opportunity costs. The real risk-free interest rate is the single-period interest rate for a completely risk-free security if no inflation were expected. In economic theory, the real risk-free rate reflects the time preferences of individuals for current versus future real consumption. The sum of the real risk-free interest rate and the inflation premium is the nominal risk-free interest rate. As the inflation premium is 2%, the 1% real risk-free rate is not the opportunity cost of buying the US T-bill.
B Incorrect because interest rates can be considered opportunity costs. The inflation premium compensates investors for expected inflation. The real risk-free interest rate is the single-period interest rate for a completely risk-free security if no inflation were expected. In economic theory, the real risk-free rate reflects the time preferences of individuals for current versus future real consumption. The sum of the real risk-free interest rate and the inflation premium is the nominal risk-free interest rate. As the real risk-free rate is 1%, the 2% inflation premium is not the opportunity cost of buying the US T-bill.
C Correct because interest rates can be considered opportunity costs. The real risk-free interest rate is the single-period interest rate for a completely risk-free security if no inflation were expected. In economic theory, the real risk-free rate reflects the time preferences of individuals for current versus future real consumption. The sum of the real risk-free interest rate and the inflation premium is the nominal risk-free interest rate. Many countries have governmental short-term debt whose interest rate can be considered to represent the nominal risk-free interest rate in that country. The interest rate on a 90-day US Treasury bill (T-bill), for example, represents the nominal risk-free interest rate over that time horizon. Therefore, the opportunity cost of this investment is 1% + 2% = 3%.
35. An investor invests a fixed amount of money into a fund each year for three years as follows:
| Year | Price per Share |
| 1 | 14.00 |
| 2 | 12.00 |
| 3 | 17.00 |
The investor’s average cost per share is closest to:
A. €14.05.
B. €14.33.
C. €14.63.
A Correct because the harmonic mean is used to determine the average price paid per share when using cost averaging;
The weighted mean formula could also be used, where the weights would be the proportion of the total number of shares purchased. However, in order to use this method a fixed investment amount would need to be created.
B Incorrect because it is the average price per share, not the cost per share; (14 + 12 + 17)/3 = 14.33. Using the arithmetic mean assumes equal weighting, which is not appropriate when the investment amount is fixed and the share price is variable.
C Incorrect because the price per share is incorrectly used as the weight in the weighted mean formula;
36. An investor records the following information and transactions for a stock:
| Year | Price per Share at Beginning of Year | Cash Flow at Beginning of Year |
| 1 | $100 | $100 used to purchase one share |
| 2 | $100 | $9 received in dividends and not reinvested |
| 3 | $100 | $100 received from selling one share |
The investor’s money-weighted rate of return is closest to:
A. 4.4%.
B. 4.5%.
C. 4.6%.
A Incorrect because it is the money-weighted return when the dividend is reinvested. Calculator solution: CF0 = –100, CF1 = 0, CF2 = 109, compute IRR = 4.403% ≈ 4.4%. The answer is also the geometric mean return; [(1 + 0.09)(1 + 0.00)]0.5 – 1 = 0.04403 ≈ 4.4%.
B Incorrect because it is the arithmetic mean return; (0.09 + 0.00)/2 = 0.045 = 4.5%. The arithmetic or mean return is denoted by Ri and given by the following equation for asset i, where Rit is the return in period t and T is the total number of periods: Ri = (Ri1 + Ri2 + … + RiT ) / T. The returns in Year 1 and Year 2 are calculated as (100 – 100 + 9)/100 = 0.09 and (100 – 100 + 0)/100 = 0.00, respectively.
C Correct because it is the money-weighted return when the dividend is not reinvested. Calculator solution: CF0 = –100, CF1 = 9, CF2 = 100, compute IRR = 4.601% ≈ 4.6%.
37. If a client controls the timing of cash flows into and out of a portfolio, which of the following is most appropriate when evaluating the performance of the portfolio manager?
A. Time-weighted rate of return
B. Arithmetic mean rate of return
C. Money-weighted rate of return
A Correct because the time-weighted rate of return is the preferred performance measure as it neutralises the effect of cash withdrawals or additions to the portfolio, which are generally outside of the control of the portfolio manager.
B Incorrect because the arithmetic return is biased upward. For the evaluation of portfolios of publicly traded securities, the time-weighted rate of return is the preferred performance measure.
C Incorrect because investment managers find time-weighted returns more meaningful. If a client gives an investment manager more funds to invest at an unfavourable time, the manager’s money-weighted rate of return will tend to be depressed. If a client adds funds at a favourable time, the money-weighted return will tend to be elevated. The time-weighted rate of return removes these effects.
38. The time preference of individuals for current instead of future real consumption is captured by the:
A. liquidity premium.
B. maturity premium.
C. real risk-free interest rate.
A Incorrect because the liquidity premium compensates investors for the risk of loss relative to an investment’s fair value if the investment needs to be converted to cash quickly. US T-bills, for example, do not bear a liquidity premium because large amounts can be bought and sold without affecting their market price.
B Incorrect because the maturity premium compensates investors for the increased sensitivity of the market value of debt to a change in market interest rates as maturity is extended. For example, the difference between the interest rate on longer-maturity, liquid Treasury debt and that on short-term Treasury debt reflects a positive maturity premium for the longer-term debt.
C Correct because the real risk-free rate reflects the time preferences of individuals for current versus future real consumption.
39. An investor summarises end-of-year cash outlays and proceeds from a two-year investment in a company’s shares below:
| Year | Outlays | Proceeds |
| 0 | $100 to purchase the first share | — |
| 1 | $110 to purchase the second share | $10 dividend received from first share (not reinvested) |
| 2 | — | $230 received from selling two shares at $115 per share |
The annualised time-weighted rate of return of the investment over the two-year period is closest to:
A. 9.7%.
B. 12.0%.
C. 12.3%.
A Incorrect because it is the money-weighted rate of return of the investment. The money-weighted return and its calculation are similar to the internal rate of return. The internal rate of return is the discount rate at which the sum of present values of these cash flows will equal zero. Calculator solution: [CF0] = investment in the first share = –100, [CF1] = investment in the second share + dividend from first share = –110 + 10 = –100, [CF2] = proceeds of selling two shares = 230, [IRR] [CPT] = 0.09687 ≈ 9.7%.
B Correct because the time-weighted rate of return measures the compound rate of growth of $1 initially invested in the portfolio over a stated measurement period. We find this time-weighted return by taking the geometric mean of the two holding period returns. A holding period return is the return earned from holding an asset for a single specified period of time. This return can be generalized and shown as a mathematical expression in which P is the price and I is the income: R = [(P1 – P0) + I1]/P0. The subscript indicates the time of the price or income, (t = 0), is the beginning of the period and (t = 1) is the end of the period. Thus, the holding period return between time 0 and 1 is HPR1 = [(110 – 100) + 10]/100 = 0.2 = 20%, and the holding period return between time 1 and 2 is HPR2 = [(230 – 220) + 0]/220 = 0.04545 ≈ 4.5%, where 220 = 110 × 2 is the price (value) of the two shares held by the investor at time 1. The time-weighted rate of return is then [(1 + HPR1) × (1 + HPR2)]0.5 – 1 = [(1 + 0.2) × (1 + 0.04545)]0.5 – 1 = 0.12006 ≈ 12.0%.
C Incorrect because it simply calculates the arithmetic average of the two holding period returns; (20% + 4.545%)/2 = 12.273% ≈ 12.3%.
40. An investor gathers the following information about a stock:
| Stock price at t = 0 | $20 |
| Dividend paid at t = 1 | $3 |
| Stock price at t = 1 | $12 |
| Dividend paid at t = 2 | $1 |
| Stock price at t = 2 | $20 |
The investor purchased one unit of the stock at t = 0 and sold it at t = 2. If the dividends were not reinvested, the money-weighted rate of return is closest to:
A. 10%.
B. 15%.
C. 20%.
A Correct because the money-weighted return and its calculation are similar to the internal rate of return and the yield to maturity. Just like the internal rate of return, amounts invested are cash outflows from the investor’s perspective and amounts returned or withdrawn by the investor, or the money that remains at the end of an investment cycle, is a cash inflow for the investor. For the stock investment this is: $20 = $3/(1 + r) + ($20 + $1)/(1 + r)2, yielding r = 10.24% ≈ 10%. Calculator solution: CF0 = –20; CF1 = 3; CF2 = 21; IRR CPT = 10.24.
B Incorrect because it is time-weighted, not money-weighted, rate of return. For the stock investment, the holding period returns (HPR) for the two periods are HPR1 = ($12 – $20 + $3)/$20 = –0.25 = –25% and HPR2 = ($20 – $12 + $1)/$12 = 0.75 = 75%. Hence, TWR = √(0.75 × 1.75) – 1 = 0.1456 = 14.56% ≈ 15%.
C Incorrect because it confuses the money-weighted rate of return with the ‘money returned’, i.e. the net cash flow: $20 + $3 + $1 – $20 = $4, which, on an initial investment of $20, corresponds to a 20% return; $4/$20 = 0.2 = 20%.
41. An individual can invest $19,000 today and receive $20,000 in one year’s time. If her required rate of return is 5%, the rate of return on the investment is:
A. less than the required rate of return.
B. equal to the required rate of return.
C. greater than the required rate of return.
A Incorrect because the return on the investment can be calculated as (20,000 – 19,000)/19,000 = 1,000/19,000 = 5.26%. Therefore, it is greater (not less) than the required return of 5%.
B Incorrect because the return on the investment can be calculated as (20,000 – 19,000)/19,000 = 1,000/19,000 = 5.26%. Therefore, it exceeds (not is equal to) the required return of 5%.
C Correct because the return on the investment can be calculated as (20,000 – 19,000)/19,000 = 1,000/19,000 = 5.26%. Therefore, it exceeds the required return of 5%.
42. An analyst collects the following set of ten returns from previous years:
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Return(%) | 2.2 | 6.2 | 8.9 | 9.3 | 10.5 | 11.7 | 12.3 | 14.1 | 15.3 | 18.4 |
The geometric mean return is closest to:
A. 9.62%.
B. 10.80%.
C. 10.89%.
A Incorrect because it uses the geometric mean formula, not the geometric mean return formula:
B Correct because the geometric mean return is calculated as the Tth root of the product of T terms, where the terms are one plus the returns and T is the number of returns. After taking the Tth root, subtract one:
where
RG = the geometric mean return
T = the number of returns
Rt = the return in year t
C Incorrect because it is the arithmetic mean not the geometric mean return:
43. Over a period of 16 months, an investor has earned a return of 12%. The investor’s annualised return is closest to:
A. 8.87%.
B. 9.00%.
C. 9.38%.
A Correct because the annualised return is calculated using the formula for annualised return, Rannual = (1+Rperiod)c, where:
Rperiod = 12%
c = 12/16, because one year contains 12/16th of a 16-month period.
Plugging in the numbers:
Rannual = 1.12(12/16) – 1 = 0.0887 or = 8.87%
B Incorrect because the return is incorrectly calculated as 12% × 12/16 = 9.00%.
C Incorrect because the return is incorrectly calculated as (1 + 0.12/16)12 – 1= 1.007512 – 1 = 9.38%.
44. An investor observed the following hedge fund return data.
| Year | Beginning of Year Account Balance | Net Return of the Fund |
| 1 | $30 million | 10% |
| 2 | $40 million | -5% |
| 3 | $30 million | -5% |
The money-weighted return is closest to:
A. –1.523%.
B. –0.749%.
C. –0.524%.
A Incorrect. It uses cash flows from the difference of new balance at the beginning of year: CF0 = –30, CF1 = –40 + 30 = –10, CF2 = –30 + 40 = +10, CF3 = +28.5; IRR = –1.523%.
B Incorrect. It uses CF0 = –30, CF1 = –7, CF2 = +8 + 28.5 = +36.5; IRR = –0.749%.
C Correct. Tabulate the annual returns and the investment amounts to determine the cash flows:
| Year | 1 | 2 | 3 |
| Balance from previous year | 0 | 33.00 | 38.00 |
| New Investment by Maria Delanie | 30.00 | 7.00 | 0 |
| Withdrawal by Maria Delanie | 0 | 0 | –8.00 |
| Net balance at the beginning of the year | 30.00 | 40.00 | 30.00 |
| Investment return for the year | 10% | –5% | –5% |
| Investment gain (loss) | 3.00 | –2.00 | –1.50 |
| Balance at the end of the year | 33.00 | 38.00 | 28.50 |
CF0 = –30, CF1 = –7, CF2 = +8, CF3 = +28.5; IRR = –0.524%
45. A pension fund needs to pay a lump sum $10,000,000 to its participants in 15 years. If the fund is expected to earn 5% per year compounded semi-annually, the amount needed today to meet its liability in 15 years is closest to:
A. $4,767,427.
B. $4,810,171.
C. $4,892,771.
A Correct because using the equation PV = FVN (1 + rs/m)–Nm
where
m = number of compounding periods per year
rs = quoted annual interest rate
N = number of years
we compute PV = $10,000,000 × (1 + 0.05/2)–15×2 = $4,767,426.85 ≈ $4,767,427.
In applying the equation, we use the periodic rate (in this case, the semi-annual rate) and the appropriate number of periods with semi-annual compounding.
Alternative solution using a financial calculator in END mode:
N = 30; I/Y = 0.025; PMT = 0; FV = 10,000,000; CPT PV = $4,767,426.852 ≈ $4,767,427
B Incorrect because when computing present value, it uses 5% instead of EAR to get $10,000,000 × (1.05)–15 = $4,810,170.98 ≈ $4,810,171.
C Incorrect because in the present value equation, it incorrectly accounts for compounding (multiplies by 2 instead of dividing) and does not use the appropriate number of periods for semi-annual compounding (divides by 2 instead of multiplying by 2); to incorrectly compute PV = 10,000,000 × (1 + 0.05×2)–15/2 = $4,892,770.68 ≈ $4,892,771.
46. A company estimates its revenue will be 50% higher than today in four years’ time. The compound annual growth rate is closestto:
A. 10.7%.
B. 11.8%.
C. 12.5%.
A Correct because a growth rate (g) is calculated as g = (FVN/PV)1/N – 1, where FV is the future value, PV is the present value and N is the number of periods. Here, g = (1.5/1)1/4 – 1 = 0.10668 ≈ 10.7%.
B Incorrect because it is calculated as ln(1 + 0.5/4) – 1 = ln(1.125) – 1 = 0.11778 ≈ 11.8%.
C Incorrect because it is calculated as: 50%/4 = 12.5%.
47. An investor considers the following certificates of deposit (CDs) available for purchase at face value:
| CD | Interest Rate |
| 1 | 2.2% |
| 2 | 3.3% |
| 3 | 4.4% |
If each CD has the same maturity and default risk, the opportunity cost of investing in CD 1 is closest to:
A. 0.0%.
B. 1.1%.
C. 2.2%.
A Incorrect because the investor is foregoing higher rates of return by investing in the security with the lowest return.
B Incorrect because 1.1% is not the most the investor is foregoing; however, it is the difference if incorrectly using the average return of the three securities.
C Correct because all three securities have the same maturity and default risk so the investor is forgoing 2.2% (4.4% – 2.2%) by investing in CD 1 rather than investing in CD 3.
48. A bank offers a savings account with a stated annual rate of 3% in the first year and 5% in the second year. If returns are compounded quarterly and €90,000 is deposited in the account at the beginning of the first year, the account’s value at the end of the second year is closest to:
A. €97,200.
B. €97,335.
C. €97,455.
A Incorrect because it fails to account for any compounding; (3% + 5%) = 8%; 90,000(1.08) = 97,200.
B Incorrect because it fails to account for quarterly compounding; 90,000(1.03)(1.05) = 97,335.
C Correct because the returns are compounded quarterly;
49. An investor is considering two term deposits with the following characteristics:
| Term Deposit 1 | Term Deposit 2 | |
| Compounding frequency | Quarterly | Continuous |
| Stated annual rate | 4% | — |
The stated annual rate for Term Deposit 2 that should make the investor indifferent between the two term deposits is closestto:
A. 3.92%.
B. 3.98%.
C. 4.06%.
A Incorrect because it takes the natural logarithm of Term Deposit 1’s stated annual rate instead of its effective annual rate (EAR). Calculation: ln(1.04) = 0.039221 = 3.92%.
B Correct because the investor will be indifferent if the EAR for both term deposits is the same. Therefore, we need to find the stated annual rate with continuous compounding that corresponds to the EAR of the quarterly compounded term deposit. Calculations: EAR of Term Deposit 1 = (1 + 0.04/4)4 – 1 = 0.040604. Hence, EAR of Term Deposit 2 = 0.040604 = er – 1, leading to a stated annual rate for Term Deposit 2 of r = ln(1.040604) = 0.039801 = 3.98%.
C Incorrect because it is the EAR of Term Deposit 1, not the stated annual rate of Term Deposit 2. EAR of Term Deposit 1 = (1 + 0.04/4)4 – 1 = 0.040604 = 4.06%. This answer is also closest to the calculations e0.04 – 1 = 0.040811 = 4.08% or e0.040604 – 1 = 0.041440 = 4.14%.
50. An analyst gathers the following information about a portfolio:
| Returns | ||
| Year | Equity | Fixed Income |
| 1 | 7.20% | 2.10% |
| 2 | 9.60% | -4.60% |
| 3 | -14.20% | 4.7% |
If the equity weighting is 70%, the fixed-income weighting is 30% and the portfolio is rebalanced annually, the portfolio’s annual geometric mean return is closest to:
A. 0.60%.
B. 0.83%.
C. 1.82%.
A Correct because the first step is to calculate the portfolio’s annual returns as a weighted mean of the equity and fixed-income returns with 70% equity and 30% fixed-income weighting.
Year 1: (0.7 ´ 0.072) + (0.3 ´ 0.021) = 0.0567 = 5.67%
Year 2: (0.7 ´ 0.096) + (0.3 ´ –0.046) = 0.0534 = 5.34%
Year 3: (0.7 ´ –0.142) + (0.3 ´ 0.047) = –0.0853 = –8.53%
Next, the portfolio’s geometric mean annual return is calculated as:
[(1 + 0.0567) ´ (1 + 0.0534) ´ (1 – 0.0853)]^(1/3) – 1 = [1.01818]^(1/3) – 1 = 0.00602 » 0.60%.
B Incorrect because it reflects the incorrect decision to calculate the arithmetic mean return of the portfolio in the second step.
Annual portfolio returns:
Year 1: (0.7 ´ 0.072) + (0.3 ´ 0.021) = 0.0567 = 5.67%
Year 2: (0.7 ´ 0.096) + (0.3 ´ –0.046) = 0.0534 = 5.34%
Year 3: (0.7 ´ –0.142) + (0.3 ´ 0.047) = –0.0853 = –8.53%
Next, the portfolio’s arithmetic mean annual return is calculated as:
(0.0567 + 0.0534 – 0.0853)/3 = 0.00827 » 0.83%.
C Incorrect because it reflects the error of not applying the cubed root when the three annual returns are linked geometrically in the second step.
Annual portfolio returns:
Year 1: (0.7 ´ 0.072) + (0.3 ´ 0.021) = 0.0567 = 5.67%
Year 2: (0.7 ´ 0.096) + (0.3 ´ –0.046) = 0.0534 = 5.34%
Year 3: (0.7 ´ –0.142) + (0.3 ´ 0.047) = –0.0853 = –8.53%
Next, the portfolio’s cumulative return is calculated as:
[(1 + 0.0567) ´ (1 + 0.0534) ´ (1 – 0.0853)] – 1 = 1.01818 – 1 = 0.01818 » 1.82%
51. An investor purchased a stock for $450 and then sold the stock immediately after receiving a dividend of $2. If the holding period return is a loss of 10.2%, the investor sold the stock at a price closest to:
A. $402.
B. $404.
C. $406.
A Correct because a holding period return is the return earned from holding an asset for a single specified period of time. This return can be generalised and shown as a mathematical expression in which P is the price and I is the income: R= [(P1 – P0) + I1]/P0. The subscript indicates the time of the price or income, (t = 0), is the beginning of the period and (t = 1) is the end of the period. Hence, P1 = R × P0 + P0 – I1 = –10.2% × $450 + $450 − $2 = $402.1 ≈ $402.
B Incorrect because if the stock was sold for $404, the holding period return would be ($404 – $450 + $2)/$450 = –9.8%. The incorrect price of $404 ignores the impact of the dividend; holding period return (HPR) = (P1 − P0)/P0; P1 = HPR × P0 + P0 = –10.2% × $450 + $450 = $404.1 ≈ $404.
C Incorrect because if the stock was sold for $406, the holding period return would be ($406 – $450 + $2)/$450 = –9.3%. The incorrect price of $406 incorrectly subtracts the dividend; holding period return (HPR) = [(P1 − P0) – I1]/P0; P1 = HPR × P0 + P0 + I1 = –10.2% × $450 + $450 + $2 = $406.1 ≈ $406.
52. An investor purchases a stock for $100. Immediately after receiving a dividend of $7, the investor sells the stock for $107. The holding period return of the investment is closest to:
A. 0%.
B. 7%.
C. 14%.
A Incorrect because it incorrectly subtracts the dividend instead of adding it, and thus calculates HPR = ($107 – $100 – $7)/$100 = $0/$100 = 0%. The same result is obtained if the holding period return is calculated as R = ($100 – $107 + $7)/$107 = $0/$107 = 0%.
B Incorrect because it omits the dividend and calculates R = ($107 – $100)/$100 = $7/$100 = 7%. It is also the ratio of the dividend received over the initial investment; $7/$100 = 7%.
C Correct because a holding period return is the return earned from holding an asset for a single specified period of time. This return can be generalised and shown as a mathematical expression in which P is the price and I is the income: R = (P1 − P0 + D1)/P0 Thus, R = ($107 – $100 + $7)/$100 = $14/$100 = 14%.
53. Which of the following statements is most accurate? The money-weighted return:
A. ignores cash withdrawals and additional cash investments.
B. measures what the investor actually earned on the funds invested.
C. should be used to compare the performance of different investment managers.
A Incorrect because the money-weighted return and its calculation are similar to the internal rate of return and the yield to maturity. Just like the internal rate of return, amounts invested are cash outflows from the investor’s perspective and amounts returned or withdrawn by the investor, or the money that remains at the end of an investment cycle, is a cash inflow for the investor. That is, cash withdrawals and investments are included in the money-weighted return calculation; however, cash withdrawals and investments are ignored in the calculation of the arithmetic and geometric mean returns.
B Correct because the money-weighted return is an accurate measure of what the investor actually earned on the money invested.
C Incorrect because although the money-weighted return is an accurate measure of what the investor actually earned on the money invested, it is limited in its applicability to other situations. For example, it does not allow for return comparison between different individuals or different investment opportunities. Two investors in the same mutual fund may have different money-weighted returns because they invested different amounts in different years.
54. Which of the following risk premiums compensates investors for the risk of loss relative to an investment’s fair value if the investment needs to be converted to cash quickly?
A. Liquidity premium
B. Inflation premium
C. Maturity premium
A Correct because the liquidity premium compensates investors for the risk of loss relative to an investment’s fair value if the investment needs to be converted to cash quickly.
B Incorrect because the inflation premium compensates investors for expected inflation and reflects the average inflation rate expected over the maturity of the debt.
C Incorrect because the maturity premium compensates investors for the increased sensitivity of the market value of debt to a change in market interest rates as maturity is extended, in general (holding all else equal).
55. With respect to portfolio return measures, which of the following statements is most accurate?
A. The time-weighted return is sensitive to additions and withdrawals of funds
B. The calculations of the money-weighted return and internal rate of return are similar
C. The money-weighted return is the preferred measure when evaluating the performance of a portfolio manager
A Incorrect because an investment measure that is not sensitive to the additions and withdrawals of funds is the time-weighted rate of return.
B Correct because the money-weighted return accounts for the money invested and provides the investor with information on the return she earns on her actual investment. The money-weighted return and its calculation are similar to the internal rate of return and the yield to maturity.
C Incorrect because, for the evaluation of portfolios of publicly traded securities, the time-weighted rate of return is the preferred performance measure as it neutralises the effect of cash withdrawals or additions to the portfolio, which are generally outside of the control of the portfolio manager.









