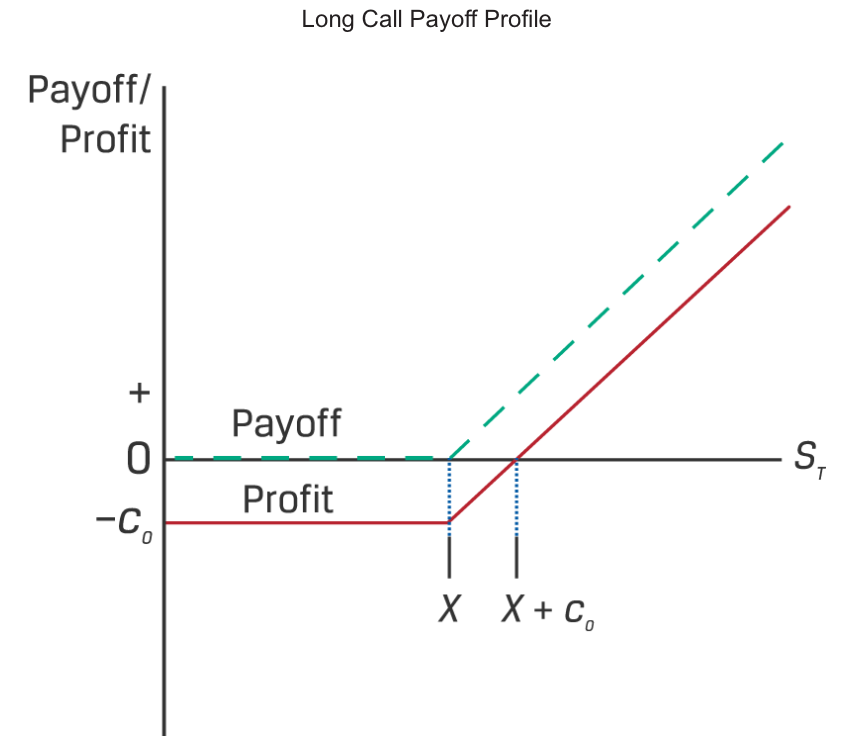
The option buyer pays a call option premium, c0, at time t = 0 to the option seller and has the right to purchase the underlying, ST , at an exercise price of X at time t = T. The exercise payoff (ST – X) is positive if ST > X and zero if ST ≤ X. The call option value at maturity, cT ,
The call option buyer’s profit equals the payoff minus the call premium, c0
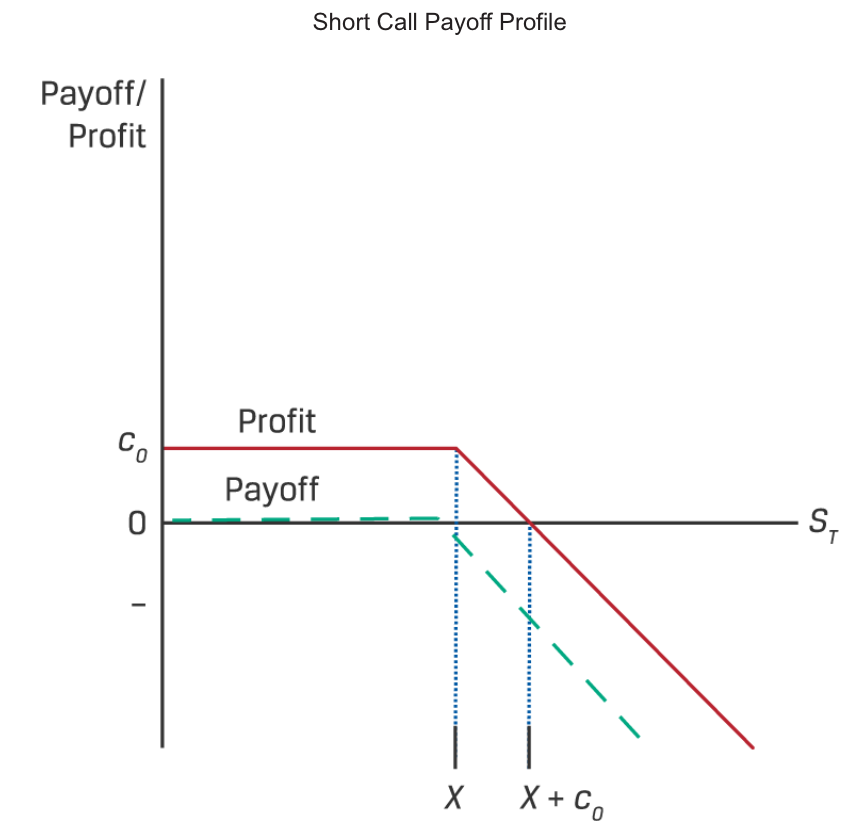
This asymmetric payoff profile is a common feature of contingent claims, which are sometimes referred to as non-linear derivatives.
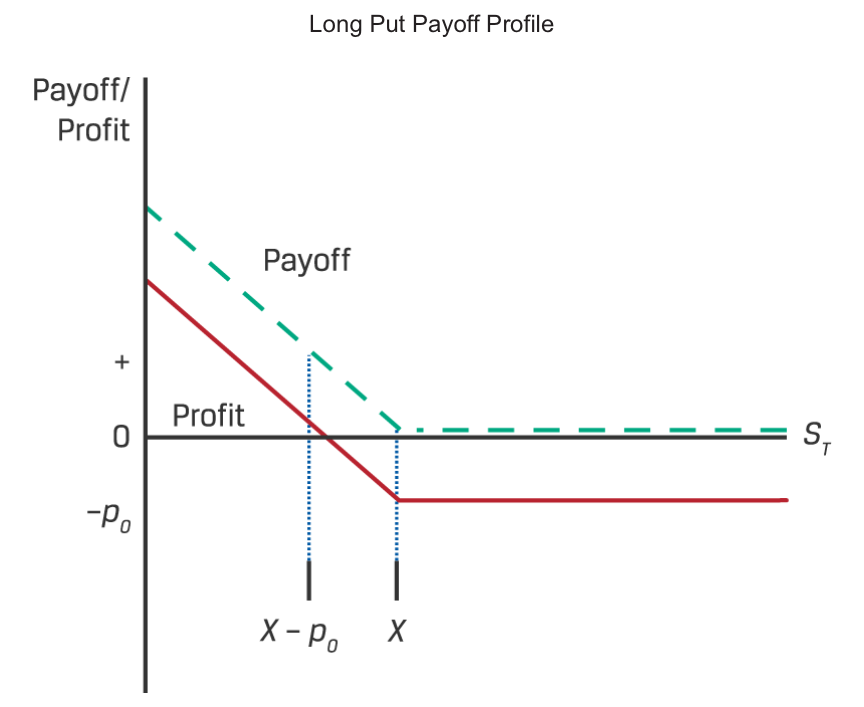
The put option buyer pays a premium of p0 at inception to the option seller and will exercise the option only if (X – ST ) > 0. As in Equations 1 and 2, we may show the long put option payoff and profit, Π, as follows:
The payoff or profit from a put option seller’s perspective is the opposite of the put option buyer’s gain or loss for a given underlying price at expiration. As in the case of the call option seller, the put option seller has a maximum gain equal to the premium. However, although a call option seller faces unlimited potential loss as the underlying appreciates beyond the exercise price, the put option seller’s loss is usually limited because the underlying price cannot fall below zero. The short put option payoffand profit are as follows:









