In hypothesis testing, we test to determine whether a sample statistic is likely to come from a population with the hypothesised value of the population parameter.
The Process of Hypothesis Testing
A hypothesis is a statement about one or more populations that we test using sample statistics.
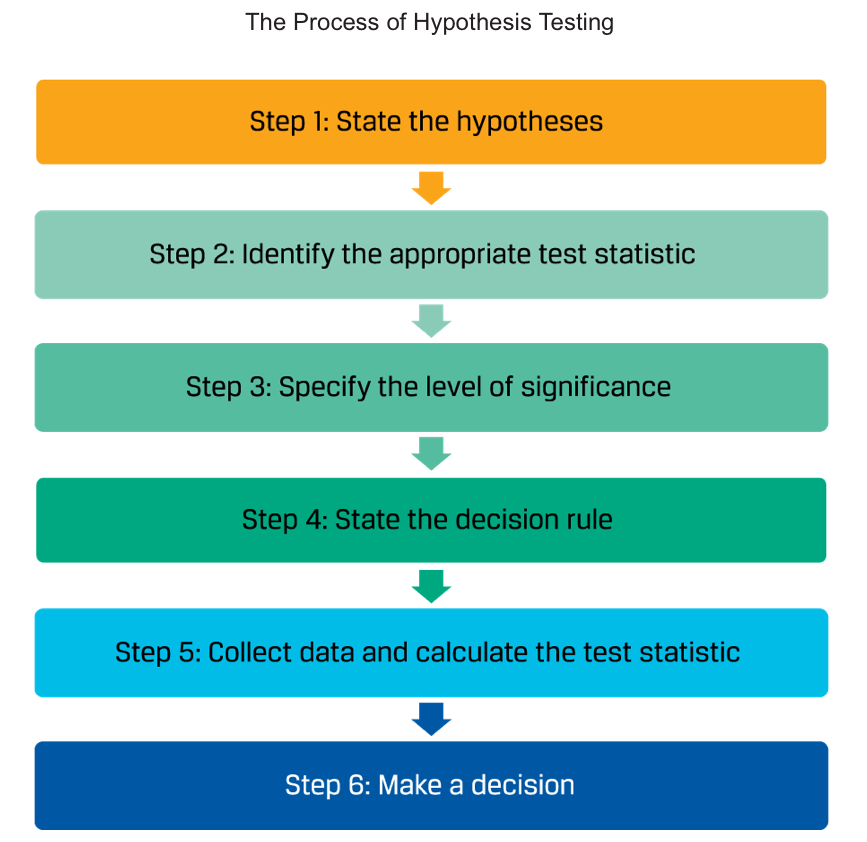
Stating the Hypotheses
Null hypothesis (or null), designated .
Alternative hypothesis, designated .
The null hypothesis is a statement concerning a population parameter or parameters considered to be true unless the sample we use to conduct the hypothesis test gives convincing evidence that the null hypothesis is false.
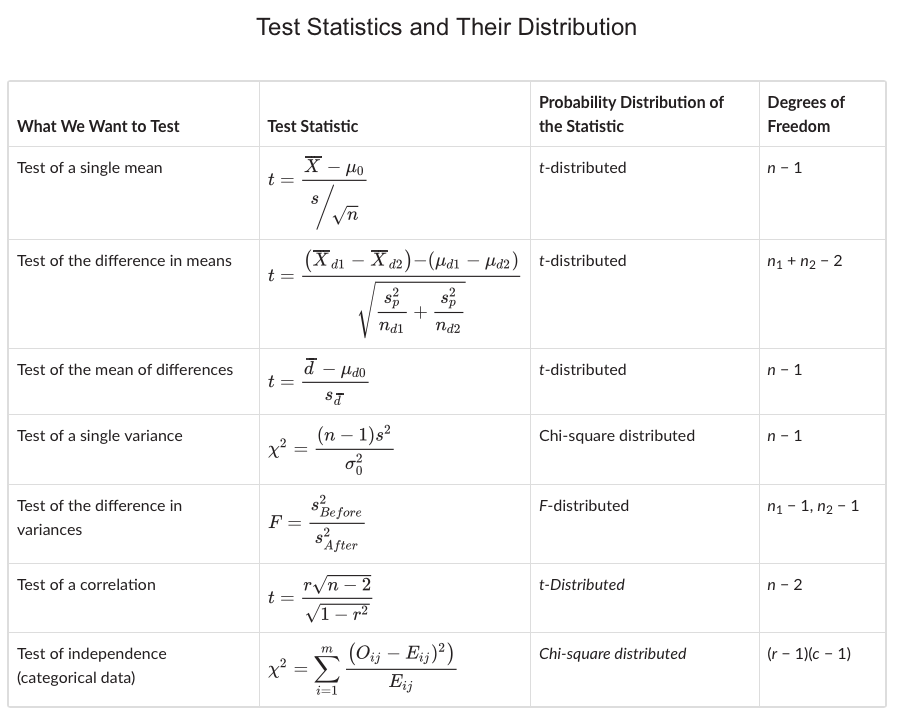
Identify the Appropriate Test Statistic and Distribution
Specify the Level of Significance
A Type I error is a false positive (reject when the null is true).
A Type II error is a false negative (fail to reject when the null is false).
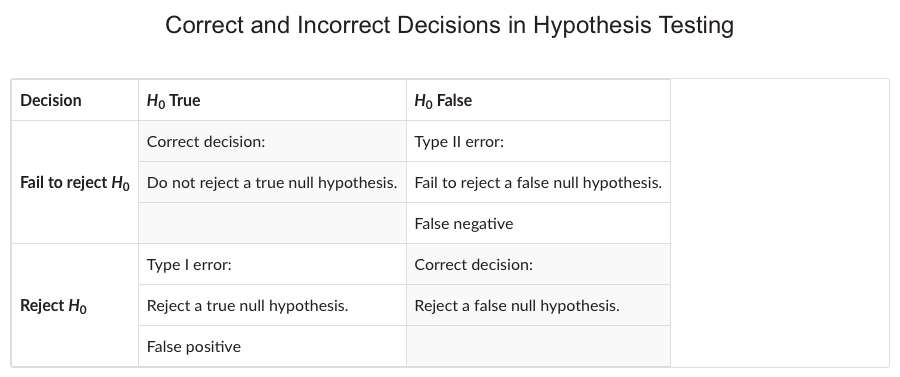
The probability of a Type I error is denoted by the lowercase Greek letter alpha, α. This probability is also known as the level of significance of the test, and its complement, (1 − α), is the confidence level.
The power of a test is the probability of correctly rejecting the null—that is, the probability of rejecting the null when it is false. The power of a test is the complement of the Type II error.
The probability of a Type II error is often denoted by the lowercase Greek letter beta, β.

State the Decision Rule
The critical value or values we choose are based on the level of significance and the probability distribution associated with the test statistic.









