Correlation between Two Variables

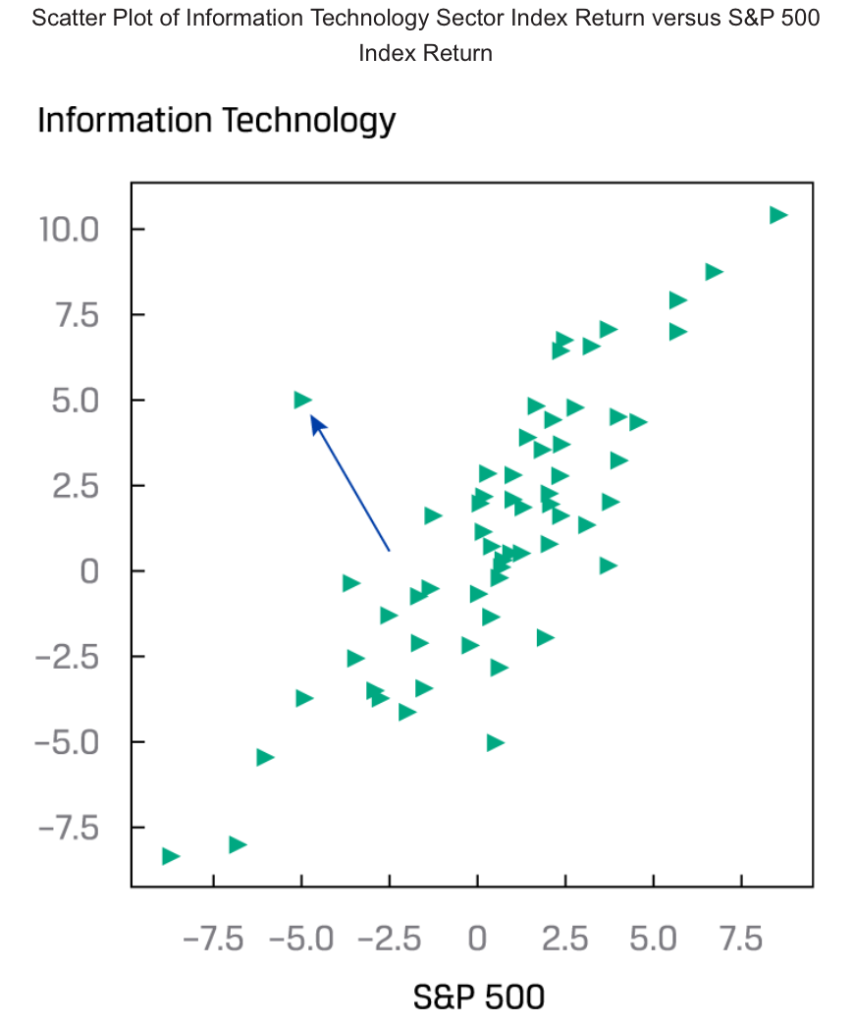
Scatter Plot

Covariance and Correlation

Correlation is a measure of the linear relationship between two random variables.

The sample covariance ($s_{XY}$) is a measure of how two variables in a sample move together:

The sample correlation coefficient is a standardised measure of how two variables in a sample move together. The sample correlation coefficient ($r_{XY}$) is the ratio of the sample covariance to the product of the two variables’ standard deviations:

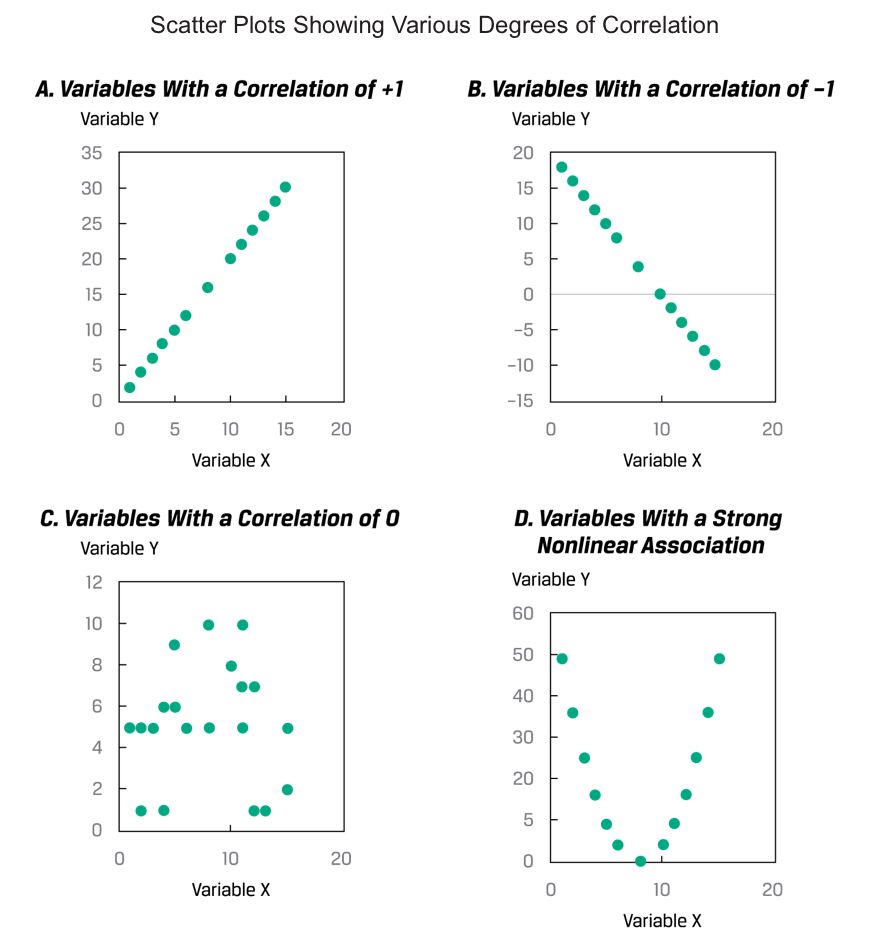
Properties of Correlation

1. Correlation ranges from -1 and +1 for two random variables, X and Y: $-1 \leq r_{XY} \leq +1$.
2. A correlation of 0, termed uncorrelated, indicates an absence of any linear relationship between the variables.
3. Apositive correlation close to -1 indicates a strong positive linear relationship. A correlation of 1 indicates a perfect linear relationship.
4. A negative correlation close to -1 indicates a strong negative (i.e., inverse) linear relationship. A correlation of -1 indicates a perfect inverse linear relationship.

Limitations of Correlation Analysis

The term spurious correlation has been used to refer to:

• correlation between two variables that reflects chance relationship in a particular dataset;
• correlation induced by a calculation that mixes each of two variables with a third variable; and
• correlation between two variables arising not from a direct relation between them but from their relation to a third variable.