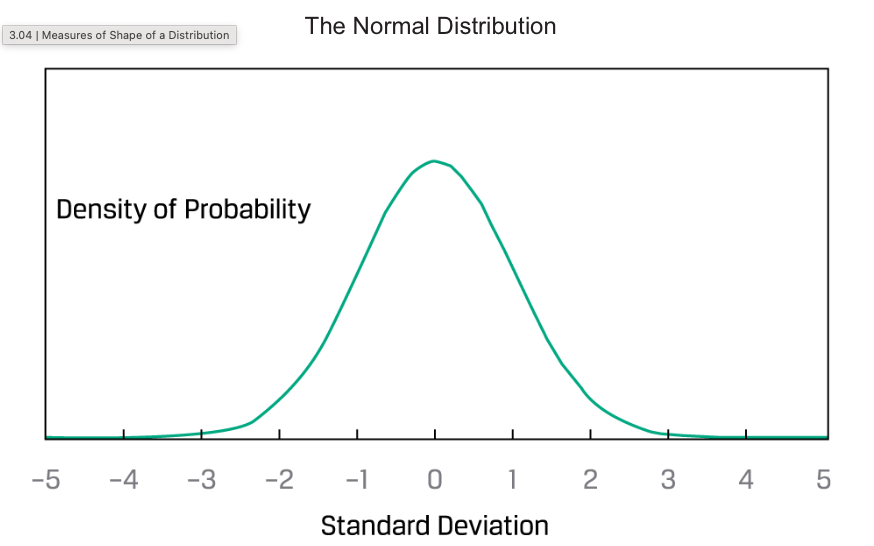
Normal distribution, this symmetrical, bell-shaped distribution plays a central role in the mean-variance model of portfolio selection; it is also used extensively in financial risk management.
The normal distribution has the following charactristics:
- Its mean, median and mode are equal.
- It is completely described by two parameters — its mean and variance (or standard deviation).
Skewness
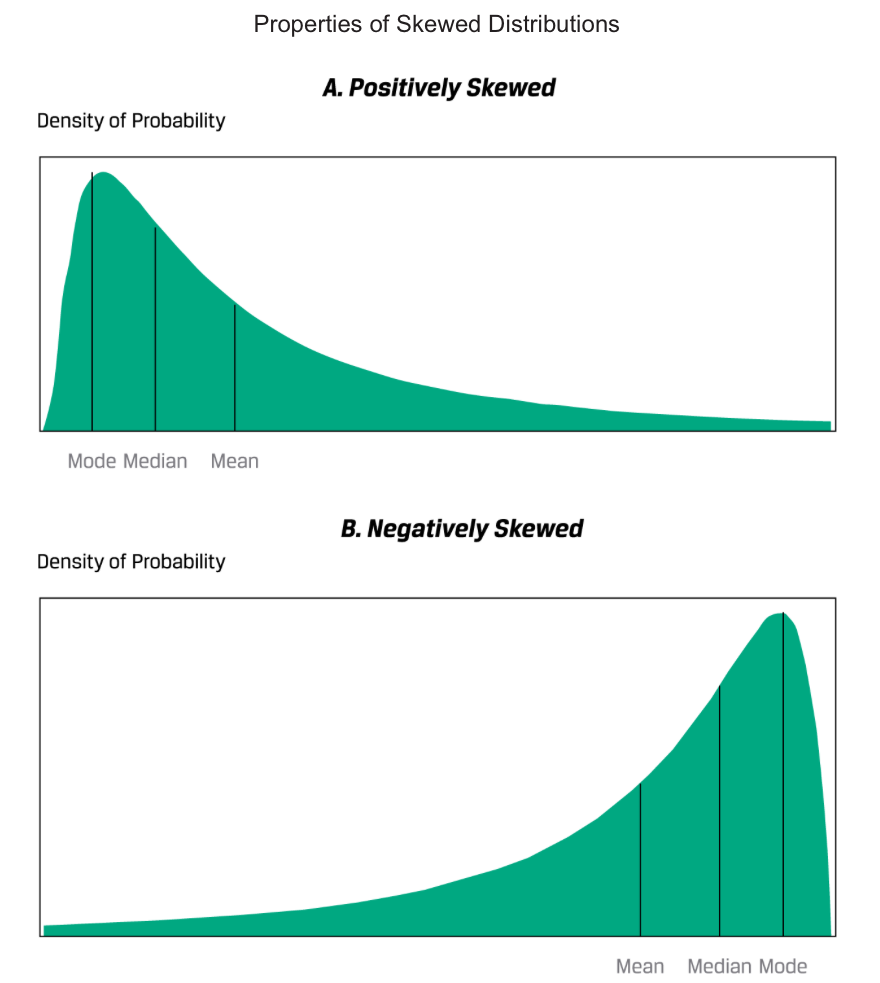
A distribution that is not symmetrical is termed skewed.
A return distribution with positive skew has frequent small losses and a few extreme gains.
A return distribution with negative skew has frequent small gains and a few extreme losses.
Skewness (sometimes referred to as relative skewness) is computed as the average cubed deviation from the mean, standardised by dividing by the standard deviation cubed to make the measure free of scale.
The approximation for computing sample skewness when n is large (100 or more) is:
Kurtosis
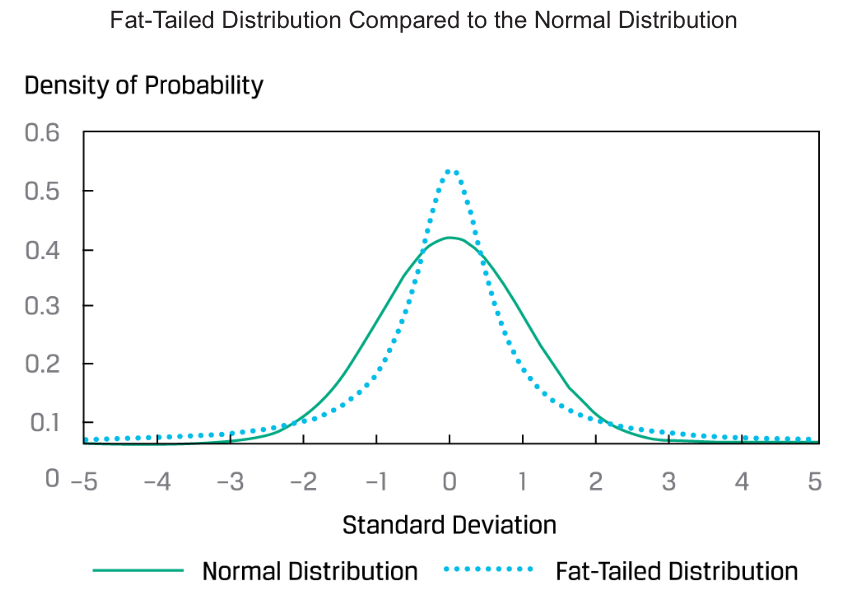
Kurtosis is a measure of the combined weight of the tails of a distribution relative to the rest of the distribution.
A distribution that has fatter tails than the normal distribution is referred to as leptokurtic or fat-tailed; a distribution that has thinner tails than the normal distribution is referred to as being platykurtic or thin-tailed; and a distribution similar to the normal distribution as it concerns relative weight in the tails is called mesokurtic.
A fat-tailed (thin-tailed) distribution tends to generate more frequent (less frequent) extremely large deviations from the mean than the normal distribution.
Excess kurtosis is the kurtosis relative to the normal distribution. For a large sample size (n=100 ore more), sample excess kurtosis () is approximately as follows:









